Spiral cracks in drying precipitates

 

We study the slow generation of crack networks as a problem of pattern formation. Issues of pattern selection and the associated statistical properties
are addressed. A typical situation involves the nucleation and propagation of cracks in an overlayer on a frictional substrate. Competition between stress concentration at crack tips and pinning effect by friction leads to a cellular, hierarchical pattern of cracks. Such patterns have a morphology apparently insensitive to the length scales of the system and the microscopic properties of the material--they all "look" the similar, from microns to kms.		 crack on mud
Under non-uniform stresses (external stress imposed locally rather than homogeneously), however, instead of generating a network the crack propagates in a preferred direction to maximize stress relief. This often leads to curved crack paths. By desiccating thin layers of precipitates, we obtain unusual fascinating forms such as these, and in particular regular spirals[1]:
exotic crack patterns
spiral crack
Move pointer over to zoom in
In a nutshell, we believe that this symmetry-breaking fracturing mode arises by the following mechanism[1], illustrated in the cartoon below: Progressive drying leads to a gradient of stresses across the thickness, as a result the layer folds up and detaches from the substrate, with a front shrinking in time (red circle below). Since stresses are concentrated around the front, when a crack is nucleated it tends to run along the front, giving rise to a spiral. Fittings of experimental and simulation data show that the spirals are logarithmic[2], corresponding to constant angular deviation from a circular crack path. We show that this occurs generally when the crack speed is proportional to the propagating speed of stress front.
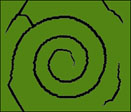simulationIncorporating this mechanism into a computer simulation using a discrete spring-block model successfully reproduces the observed spirals.

 

 

In a seashell (nautilus and ammonites), logarithmic spirals are ubiquitous albeit formed by an entirely different mechanism.
nautilus
Nautilus: move pointer over to see a log-spiral fit

References
  1. Spiral cracks without twisting,
    K.-t. Leung, L. Jozsa, M. Ravasz and Z. Neda, Nature 410, 166 (2001).
    Also e-print cond-mat/0103221. (Listed in Complexity Digest, and in Econophysics Forum)
  2. Spiral cracks in drying precipitates,
    Z. Neda, K.-t. Leung, L. Jozsa, M. Ravasz, Phys. Rev. Lett. 88, 095502 (2002).
    Also e-print cond-mat/0201272.
  3. A multimedia presentation: 1 minute Flash swf file(2.4MB), best viewed on full screen (on IE browser, hit F11).
Last updated October 11, 2002 ©KtL